Nutzung einer Small Area-Methode zur Schätzung von durchschnittlichen Bestandsmieten auf Gemeindeebene

Seitens verschiedener Nutzergruppen amtlicher statistischer Ergebnisse wird zunehmend ein Bedarf an verlässlichen Auswertungen auf möglichst kleinräumiger Ebene formuliert. Insbesondere bei Stichprobenerhebungen liegen auf kleinräumiger Ebene jedoch häufig zu wenige Daten vor, um hieraus Ergebnisse ableiten zu können, die den hohen qualitativen Ansprüchen der amtlichen Statistik genügen. Small Area-Methoden können eine Möglichkeit bieten, um trotz weniger Informationen aus einer vorliegenden Stichprobe Ergebnisse auf kleinräumiger Ebene zu veröffentlichen.

Die grundlegende Funktionsweise der Small Area-Schätzung – genauer gesagt: des in unserer Analyse verwendeten Fay-Herriot-Modells – wird im Folgenden anhand unseres Anwendungsbeispiels zur Schätzung der durchschnittlichen Bruttokaltmiete pro m² für alle Gemeinden in Nordrhein-Westfalen für die Jahre 2018 und 2022 auf Basis des Mikrozensus möglichst intuitiv auch für Interessierte ohne spezielles statistisches Hintergrundwissen erläutert. Anhand der Darstellungen in den aufklappbaren Elementen erhalten methodisch Interessierte zudem Einblick in die statistisch-formale Methodik der Small Area-Schätzung.

Für welche Situationen kann eine Small Area-Schätzung nützlich sein?

Bei der Planung einer Stichprobenerhebung wird festgelegt, für welche regionalen Ebenen auf Basis der gewonnenen Stichprobeninformationen Ergebnisse hochgerechnet und veröffentlicht werden sollen. Anhand dieser Festlegung wird dann ein Stichprobenumfang berechnet, der für alle für die Veröffentlichung vorgesehenen regionalen Ebenen eine hohe Ergebnisqualität sicherstellt. Die Stichprobe des Mikrozensus ist beispielsweise so konzipiert, dass in jedem Berichtsjahr etwa ein Prozent der Haushalte befragt wird und daraus verlässliche Ergebnisse bis auf Kreisebene hochgerechnet werden können.

Small Area-Methoden können nützlich sein, wenn auf Basis einer Stichprobe Auswertungen auf einer tieferen regionalen Ebene erfolgen sollen als durch die Stichprobenkonzeption ursprünglich vorgesehen ist. Viele gängige Methoden stoßen hier an ihre Grenzen: Bricht man z. B. den Stichprobenumfang des Mikrozensus von der Kreisebene auf die Gemeindeebene herunter, so liegen für viele Gemeinden zu geringe Stichprobenumfänge vor, um daraus verlässliche Ergebnisse abzuleiten. Daher verzichtet die amtliche Statistik im Allgemeinen auf die Veröffentlichung von Gemeindeergebnissen auf Basis des Mikrozensus. Small Area-Methoden können Abhilfe für das Problem zu geringer Stichprobenumfänge schaffen.

Auf welchem Grundprinzip basiert die Small Area-Schätzung?

Eine Small Area-Schätzung beruht auf dem sog. Borrowing Strength-Prinzip: Neben den vorhandenen (teilweise wenigen) Stichprobeninformationen werden zusätzlich externe Informationen herangezogen, um die Qualität der Schätzergebnisse zu verbessern. Indem das Potenzial dieser zusätzlichen Informationen genutzt (wörtlich: deren „Kraft ausgeborgt“) wird, sollen die Schätzunsicherheit, die aus den zu geringen Stichprobenumfängen resultiert, verringert und die Schätzergebnisse damit stabilisiert werden.

Wie läuft eine Small Area-Schätzung ab?

Im Folgenden werden die einzelnen Schritte der Schätzmethodik des von uns verwendeten Fay-Herriot-Modells erläutert und anhand unserer Anwendung auf die Schätzung durchschnittlicher Bruttomietpreise auf Gemeindeebene auf Basis der Mikrozensus-Stichprobe veranschaulicht. In den aufklappbaren Elementen finden sich detaillierte Informationen zur statistisch-methodischen Vorgehensweise.

Schritt 1: Berechnung eines Schätzwerts aus den vorhandenen Stichprobendaten

Zunächst betrachten wir die Stichprobeninformationen, die für jede Gemeinde in der vorhandenen Stichprobe vorliegen. In unserer Anwendung zeigt sich für die 396 Gemeinden in Nordrhein-Westfalen ein sehr unterschiedliches Bild (vgl. Tabelle 1): Während große kreisfreie Städte wie Duisburg oder Essen sehr viele Stichprobeneinheiten aufweisen, liegen für viele eher kleinere Gemeinden nur sehr wenige Informationen aus der auf Kreisebene gezogenen Stichprobe des Mikrozensus vor. In wenigen Gemeinden sind sogar überhaupt keine Haushalte in die Stichprobe gezogen worden.

^{Tabelle 1: Anzahl der Haushalte in der Stichprobe des Mikrozensus 2022 je Gemeinde}

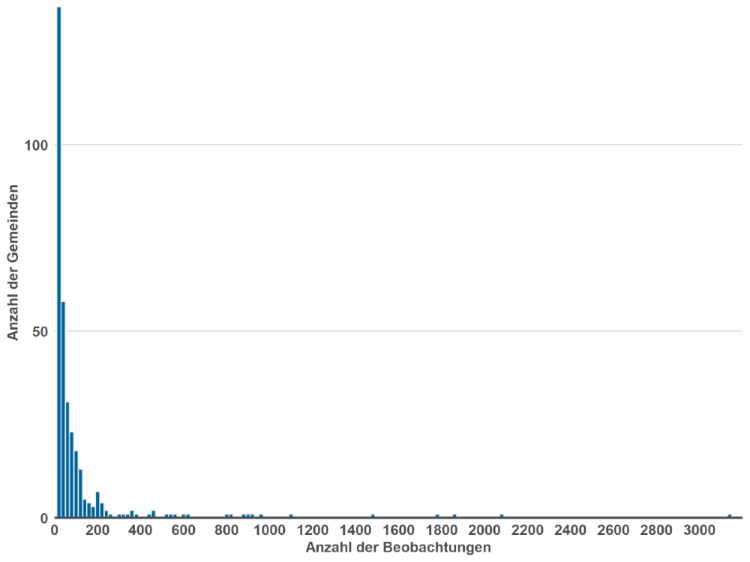
Unabhängig von der Stichprobengröße berechnen wir im ersten Schritt der Small Area-Schätzung einen Schätzwert für die durchschnittliche Bruttokaltmiete pro m² für jede Gemeinde auf Basis der vorliegenden Stichprobe. Diese geschätzten Werte bezeichnen wir im Folgenden als unsere „Stichproben-Schätzwerte“. Für ausgewählte Gemeinden sind im Vergleich der beiden Berichtsjahre 2018 und 2022 diese in Tabelle 2 dargestellt.

^{Tabelle 2: Anzahl der Haushalte in der Stichprobe des Mikrozensus 2018 und 2022, Stichproben-Schätzwerte und deren Schätzunsicherheit für den durchschnittlichen Bruttomietpreis pro m² für ausgewählte Gemeinden}

Für die amtliche Statistik ist die Messung der sog. Schätzunsicherheit ein entscheidendes Kriterium zur Beurteilung der Qualität der einzelnen Stichproben-Schätzwerte: Mit dem mittleren quadratischen Fehler* verwenden wir hierfür eine bekannte statistische Maßzahl. Kleine Werte des mittleren quadratischen Fehlers deuten dabei auf eine hohe Qualität und somit auf verlässliche Schätzergebnisse hin.

Aufgrund der stark unterschiedlichen Stichprobenumfänge in den einzelnen Gemeinden weisen die gemeindespezifischen Schätzwerte jedoch wesentliche Qualitätsunterschiede auf (vgl. Tabelle 2, Spalte „Schätzunsicherheit“). Während lediglich geringe Stichprobenfehler für die Schätzwerte für Gemeinden oder kreisfreie Städte mit hohen Stichprobenumfängen zu beobachten sind, ist die Schätzunsicherheit in den eher kleinen Gemeinden mit nur wenigen befragten Haushalten so beträchtlich, dass eine amtliche Veröffentlichung derartig unsicherer Schätzwerte nicht in Frage kommen würde.

Für Gemeinden ohne Stichprobeninformationen lässt sich kein Stichproben-Schätzwert berechnen. Wie sich für diese Gemeinden trotzdem ein valider Schätzwert berechnen lässt, wird im letzten Abschnitt dargelegt.

* Der mittlere quadratische Fehler gibt an, wie stark die mit einem bestimmten Verfahren geschätzten Werte um den gesuchten (zu schätzenden) Wert streuen. Er berücksichtigt sowohl die Verzerrung als auch die Varianz des für die Schätzung verwendeten Verfahrens.

Detaillierte methodische Erläuterung zu Schritt 1

Aus methodischer Sicht handelt es sich bei den in diesem Schritt berechneten Stichproben-Schätzwerten lediglich um gewichtete Mittelwerte. Hierfür wird der sog. Horvitz-Thompson-Schätzer verwendet:

Um für jede Gemeinde $i$ aus der jeweils vorliegenden Stichprobe $S_{i}$ den Stichproben-Schätzwert ${\hat{μ}}_{i}^{S}$ zu berechnen, werden neben den in der Stichprobe vorliegenden Datenpunkten $Y_{k}, k = 1, . . ., N_{i}$ zudem die jeder Stichprobeneinheit zugehörigen Hochrechnungsfaktoren $p_{k}$ herangezogen. Der Schätzwert für die mittlere Bruttokaltmiete pro m² ergibt sich dann durch

{\hat{μ}}_{i}^{S} = \sum_{k \in S_{i}}^{} \frac{Y_{k}}{N_{i} \cdot p_{k}}

Die so entstehenden Stichproben-Schätzwerte sind unverzerrt für die Schätzung des gemeindespezifischen Mittelwertes, können jedoch hohe Standardfehler bzw. einen hohen mittleren quadratischen Fehler aufweisen.

Schritt 2: Einbeziehung der externen Informationen

Die Grundidee der Small Area-Schätzung besteht darin, die Schätzunsicherheit unserer Schätzwerte auf Gemeindeebene zu verringern, indem zusätzlich externe Informationen für die Schätzung herangezogen werden. Für die Umsetzung dieser Grundidee sind zwei Aspekte zu berücksichtigen: Die Auswahl der externen Merkmale sowie deren methodische Einbeziehung.

Bei der Auswahl von externen Informationen sollten zunächst Vorüberlegungen getroffen werden, welche verfügbaren externen Kennzahlen einen potenziellen Zusammenhang zum zu schätzenden Merkmal aufweisen könnten. Außerdem ist zu beachten, dass alle in Frage kommenden Kennzahlen aggregiert auf der regionalen Ebene vorliegen müssen, für welche die Small Area-Schätzung vorgenommen werden soll.

In unserer Anwendung möchten wir den durchschnittlichen Bruttomietpreis pro m² für alle Gemeinden in Nordrhein-Westfalen schätzen. Wir nehmen in unseren Pool von externen Informationen insgesamt 37 Merkmale auf, die möglicherweise einen statistischen Zusammenhang zur Höhe des Mietpreises aufweisen und aggregiert auf Gemeindeebene verfügbar sind: z. B. verschiedene demografische und sozioökonomische Faktoren, Kennzahlen zur Bautätigkeit und zum Arbeitsmarkt sowie vergangene Wahlergebnisse. Eine Übersicht des Pools an betrachteten Hilfsvariablen findet sich im Download-Bereich.

Durch die Zusammenstellung des Pools der externen Kennzahlen treffen wir keine inhaltliche Vorfestlegung darüber, welche konkreten Kennzahlen zur Schätzung der Bruttomietpreise herangezogen werden. Die Auswahl der externen Kennzahlen, die wir für die Verbesserung der Schätzung verwenden werden, erfolgt anhand eines statistischen Selektionsverfahrens im Vorfeld der eigentlichen Schätzung. Dabei werden die Kennzahlen ausgewählt, die den stärksten messbaren Zusammenhang mit der Höhe der geschätzten durchschnittlichen Bruttomietpreise der Gemeinden aufweisen.

Selektierte Merkmale aus dem Pool externer Kennzahlen für unsere Anwendung

Aus dem von uns zusammengestellten Pool externer Informationen, die für die Schätzung der durchschnittlichen Bruttokaltmieten potenziell hilfreich sein können, hat ein statistisches Selektionsverfahren folgende Kennzahlen für die Small Area-Schätzung ausgewählt:

Einbürgerungen je Einwohnerin und Einwohner
Gestorbene je Einwohnerin und Einwohner
Anteil obdachloser Personen je Einwohnerin und Einwohner
Durchschnittlicher monatlicher Wohngeldanspruch
Wahlanteile der AfD, Grünen, Linken, FDP und Piratenpartei bei der Bundestagswahl 2021
Fertigstellungen von Wohnungen je Einwohnerin und Einwohner
Siedlungsdichte
Anteil der sozialversicherungspflichtig Beschäftigten im produzierenden Gewerbe
Anteil der über 75-Jährigen an der Bevölkerung
Anteil der Arbeitslosen

Statistische Selektionsverfahren vergleichen verschiedene Konstellationen bei der Zusammenstellung von bestimmten externen Kennzahlen miteinander und entscheiden anhand eines festgelegten Kriteriums, welche Anzahl und Auswahl an externen Kennzahlen auf Basis der vorliegenden Daten eine „bestmögliche“ Schätzung des durchschnittlichen Mietpreises ermöglichen. In unserer Anwendung haben wir als Kriterium für den Vergleich der verschiedenen Merkmalskombinationen Akaikes Informationskriterium (kurz: AIC) verwendet.

Bitte beachten Sie: Die Auswahl der Kennzahlen sollte nicht inhaltlich interpretiert werden. Das Selektionsverfahren verfolgt einen rein pragmatischen Ansatz, indem diejenigen Kennzahlen ausgewählt werden, die einen besonders hohen Zusammenhang zu den Stichproben-Schätzwerten aufweisen und somit ein möglichst hohes Potenzial zur deren Stabilisierung bieten.

Der Einbezug der externen Informationen in die Schätzung der durchschnittlichen Bruttomietpreise pro m² erfolgt über ein statistisches Modell. Dabei wird unterstellt, dass ein fixer Zusammenhang zwischen dem durchschnittlichen Bruttomietpreis und den externen Variablen besteht, der nicht auf einzelne Gemeinden beschränkt, sondern gemeindeübergreifend gültig ist. Mit Hilfe eines Regressionsmodells wird dieser Zusammenhang geschätzt.

Als Ergebnis des zweiten Schritts unserer Small Area-Schätzung halten wir Folgendes fest: Wir haben neben unseren Stichproben-Schätzwerten aus Schritt 1 nun weitere Informationen gefunden, mit denen sich die Höhe des durchschnittlichen Bruttomietpreises je m² in den einzelnen Gemeinden erklären lässt.

Detaillierte methodische Erläuterung zu Schritt 2

Die $p$ externen Merkmale, die für die Schätzung durch das Selektionsverfahren ausgewählt wurden und aggregiert auf Gemeindeebene vorliegen, werden im Folgenden mit $x_{i} = (x_{1, i}; x_{2, i}; . . ., x_{p, i})'$ bezeichnet. Um den gemeindeübergreifend gültigen Zusammenhang zwischen den Stichproben-Schätzwerten ${\hat{μ}}_{i}^{S}$ für alle Gemeinden $i$ aus Schritt 1 und den selektierten externen Merkmalen $x_{i}$ zu berechnen, wird folgendes Regressionsmodell geschätzt:

{\hat{μ}}_{i}^{S} = x'_{i} \cdot β + υ_{i} + ε_{i}

Als Resultat dieser Schätzung erhalten wir den Vektor $\hat{β} = ({\hat{β}}_{1}; {\hat{β}}_{2}; . . .; {\hat{β}}_{p})'$ der geschätzten Regressionskoeffizienten. Der Vektor $\hat{β}$ enthält alle Informationen über den Zusammenhang zwischen den Stichproben-Schätzwerten und den externen Merkmalen und quantifiziert damit den zusätzlichen Informationsgehalt, den wir zur Stabilisierung unserer Schätzungen verwenden wollen.

Es gibt zwei Störgrößen, $υ_{i}$ und $ε_{i}$ , im Regressionsmodell. Hierbei stellt $υ_{i}$ einen zufälligen Effekt mit Erwartungswert 0 dar, der die nicht durch die externen Kennzahlen erklärbare Variation der durchschnittlichen Mietpreise zwischen den einzelnen Gemeinden abbildet. Die Varianz $σ_{υ}^{2}$ dieses übergreifenden Zufallseffekts wird ebenfalls im Rahmen der Schätzung des Regressionsmodells berechnet. Außerdem bezeichnet $ε_{i}$ den zufälligen Schätzfehler mit Erwartungswert 0 und gemeindespezifischer Varianz $σ_{ε, i}^{2}$ , der durch die Schätzung der gemeindespezifischen Mietpreise in Schritt 1 entsteht.

Schritt 3: Berechnung der Small Area-Schätzwerte für alle Gemeinden

Im letzten Schritt können wir nun die eigentliche Small Area-Schätzung durchführen und einen Schätzwert für die durchschnittliche Bruttokaltmiete pro m² für jede Gemeinde berechnen. Hierzu führen wir die Ergebnisse aus den beiden vorangegangenen Schritten zusammen und berechnen den Small Area-Schätzer für jede Gemeinde als eine gewichtete Summe der gemeindespezifischen Stichproben-Schätzwerte (aus Schritt 1) und der aus den externen Kennzahlen errechneten Informationen (aus Schritt 2). Das folgende Schema veranschaulicht das Vorgehen bei der Berechnung:

Stichproben-Schätzwert für Gemeinde $i$ ⋅ Gewichtung des Stichproben-Schätzwerts

+ Gewonnene Informationen aus externen Kennzahlen ⋅ Gewichtung der externen Informationen

= Small Area-Schätzer für Gemeinde $i$

Die entscheidende Rolle bei der finalen Schätzung der Small Area-Ergebnisse spielen die Gewichte, mit denen die Stichproben-Schätzwerte und die Informationen aus den externen Kennzahlen vor der Addition multipliziert werden. Für diese gilt Folgendes:

Beide Gewichte addieren sich in Summe zu Eins. Das bedeutet: Ist die Gewichtung der Stichproben-Schätzung hoch (z. B. 0,9), erhalten die Informationen aus den externen Kennzahlen eine geringe Gewichtung (im Beispiel: 0,1).
Es handelt sich um gemeindespezifische Gewichte, d. h. jede Gemeinde $i$ weist ein individuelles Gewichtungspaar auf.
Die Gewichte errechnen sich als Anteil der Unsicherheit der Regressionsschätzung an der gesamten Unsicherheit (siehe methodische Erläuterung zu Schritt 3).

Die Gewichte geben damit für jede Gemeinde an, welchen Einfluss die Informationen aus der vorliegenden Stichprobe und die Informationen aus den externen Kennzahlen auf den Schätzwert für den durchschnittlichen Mietpreis in einer Gemeinde nehmen.

Die konkreten Gewichtungswerte stellen Indikatoren für den Grad der Verlässlichkeit unserer Stichproben-Schätzwerte dar und kommen wie folgt zustande: Weist die für eine Gemeinde vorhandene Stichprobe eine hohe Streuung bzw. eine hohe Unsicherheit auf, z. B. aufgrund nur weniger vorliegender Stichprobeneinheiten, so ist die Gewichtung der Stichproben-Schätzwerte für diese Gemeinde tendenziell gering – denn die Informationen, die wir aus den Stichproben-Schätzwerten erhalten, sind in diesem Fall relativ wenig belastbar. Gleichzeitig hätten die aus den externen Kennzahlen gewonnenen Informationen eine entsprechend hohe Gewichtung, sodass wir uns bei der Berechnung des Small Area-Schätzers in diesem Fall eher auf das Erklärungspotenzial der externen Kennzahlen stützen. Liegen allerdings sehr viele bzw. verlässliche Stichprobeninformationen in einer Gemeinde vor, so erhält der entsprechende Stichproben-Schätzwert eine hohe Gewichtung: Weil bereits geeignete Informationen aus der Stichprobe vorliegen, sind wir auf die zusätzlichen Informationen in diesem Fall weniger stark angewiesen.

Die berechneten Gewichte in unserer Anwendung bestätigen diesen Zusammenhang (vgl. Abbildung 1): Die Gewichtungen der Stichproben-Schätzwerte weisen insbesondere in den Gemeinden mit großen Stichprobenumfängen einen Wert nahe 1 auf. In diesen Fällen benötigen wir somit nur wenig Unterstützung durch die externen Kennzahlen bei der Berechnung eines verlässlichen Schätzwerts. In kleinen Gemeinden mit tendenziell wenigen vorliegenden Stichprobeneinheiten sind die Gewichtungen der Stichproben-Schätzwerte eher gering und die Gewichtung der Information aus den externen Kennzahlen folglich hoch.

^{Abbildung 1: Verteilung der berechneten Gewichte für die Stichproben-Schätzwerte für die Berichtsjahre 2018 und 2022. Die blauen Boxen visualisieren jeweils die mittleren 50 % der Verteilung der Gewichte}

Detaillierte methodische Erläuterung zu Schritt 3

Formal ergibt sich der Small Area-Schätzer ${\hat{μ}}_{i}^{S m A}$ für die durchschnittliche Bruttokaltmiete pro m² in Gemeinde $i$ durch:

{\hat{μ}}_{i}^{S m A} = w_{i} \cdot {\hat{μ}}_{i}^{S} + (1 - w_{i}) \cdot x'_{i} \cdot \hat{β}

Dabei bezeichnen ${\hat{μ}}_{i}^{S}$ den Horvitz-Thompson-Schätzer für das Stichprobenmittel aus Schritt 1, $x_{i}$ den Vektor der externen Kennzahlen für Gemeinde $i$ sowie $\hat{β}$ die geschätzten Regressionskoeffizienten aus Schritt 2. Insgesamt stellt der Ausdruck $x'_{i} \cdot \hat{β}$ die aus den externen Kennzahlen gewonnenen Informationen dar, die zusätzlich für die gemeindespezifische Schätzung der durchschnittlichen Bruttokaltmiete verwendet werden.

Das gemeindespezifische Gewicht $w_{i} \in (0; 1)$ berechnet sich aus der im Rahmen von Schritt 1 geschätzten Varianz ${\hat{σ}}_{ε, i}^{2}$ der Stichproben-Schätzwerte aus Gemeinde $i$ sowie der gemeindeübergreifenden Varianz ${\hat{σ}}_{υ}^{2}$ des Regressionsmodells aus Schritt 2:

w_{i} = \frac{{\hat{σ}}_{υ}^{2}}{{\hat{σ}}_{ε, i}^{2} + {\hat{σ}}_{υ}^{2}}

Sind alle drei Schritte durchgeführt, erhalten wir unsere gewünschten Small Area-Schätzungen für die durchschnittliche Bruttokaltmiete pro m² für jede Gemeinde in Nordrhein-Westfalen:

Schätzergebnisse

Eine Übersicht über die geschätzte Bruttokaltmiete pro m² der Berichtsjahre 2018 und 2022 für alle Gemeinden in Nordrhein-Westfalen findet sich im Download-Bereich.

Welche Möglichkeiten bestehen zur Evaluation der Schätzergebnisse?

Nachdem wir unsere Small Area-Schätzung durchgeführt haben, müssen wir das Schätzergebnis sorgfältig evaluieren. Damit stellen wir sicher, dass unsere Small Area-Schätzung einerseits erfolgreich war und außerdem keine systematischen Verzerrungen aufweist. Verzerrungen können potenziell dann entstehen, wenn bestimmte Annahmen, deren Gültigkeit für die Anwendung des hier verwendeten Small Area-Modells vorausgesetzt wurden, in der Realität nicht haltbar sind.

Zur Evaluation unserer Schätzergebnisse führen wir folgende Maßnahmen durch:

Zunächst überprüfen wir, ob wir unser Hauptziel der Small Area-Schätzung – die Stabilisierung unserer Schätzergebnisse durch die Nutzung externer Informationen – erreicht haben. Dazu berechnen wir die Schätzunsicherheit der Small Area-Schätzwerte anhand des mittleren quadratischen Fehlers und stellen diese der Schätzunsicherheit der Stichproben-Schätzwerte jeweils für die Berichtsjahre 2018 und 2022 für ausgewählte Gemeinden gegenüber:

_{Tabelle 3: Vergleich der Stichproben- und Small Area-Schätzwerte sowie der entsprechenden Schätzunsicherheit anhand des mittleren quadratischen Fehlers für ausgewählte Gemeinden, jeweils für die Berichtsjahre 2018 und 2022}

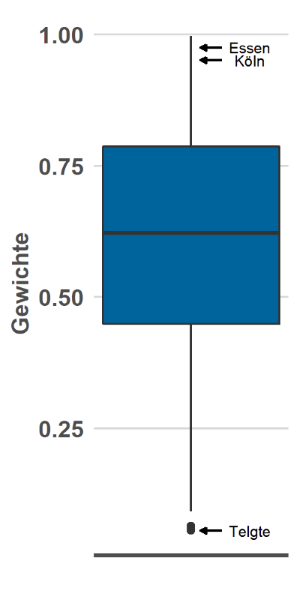
Die Ergebnisse in Tabelle 3 (bzw. der Gesamtübersicht im Download-Bereich) verdeutlichen für beide Berichtsjahre, dass die Anreicherung der Stichprobeninformationen durch die externen Kennzahlen insbesondere in den Gemeinden zu einer deutlichen Verringerung der Schätzunsicherheit führt, die eher geringe Stichprobenumfänge aufweisen (und für die in Schritt 3 der Small Area-Schätzung eine tendenziell geringere Gewichtung der Stichproben-Schätzwerte berechnet wurde, z. B. 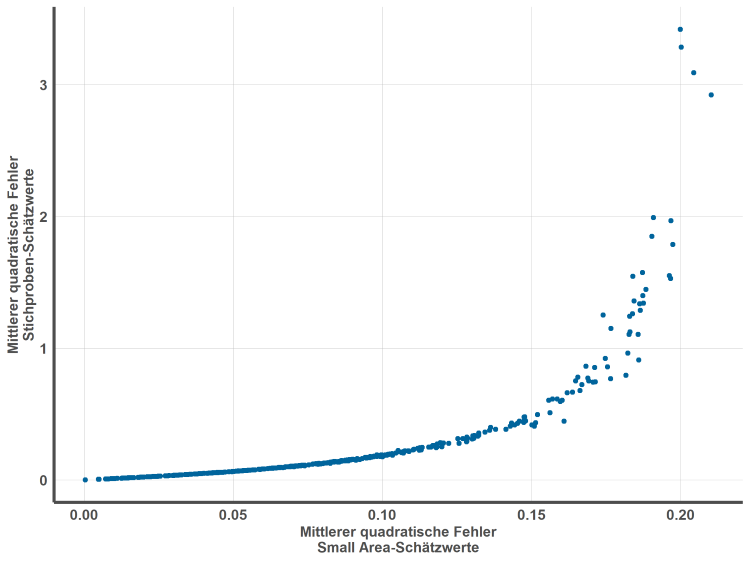Kall, Legden, Selfkant). In vielen Gemeinden und kreisfreien Städten mit hohen Stichprobenumfängen kann der mittlere quadratische Fehler jedoch nur noch geringfügig gesenkt werden: Hier liegen häufig bereits so viele Stichprobeninformationen vor, dass die Informationen aus den externen Kennzahlen nur zu einer unwesentlichen Verbesserung der Schätzung beitragen (z. B. Duisburg, Essen).

In Abbildung 2 werden die mittleren quadratischen Fehler der Small Area- und der Stichproben-Schätzwerte für alle Gemeinden in einem Streudiagramm gegenübergestellt. Hieran wird deutlich, dass die Small Area-Methodik, insbesondere bei sehr hoher Unsicherheit des Stichproben-Schätzers, zu einer deutlichen Verringerung dieser Schätzunsicherheit führt.

_{Abbildung 2: Gegenüberstellung des mittleren quadratische Fehlers für Stichproben-Schätzwerte und Small Area-Schätzwerte für das Berichtsjahr 2022}

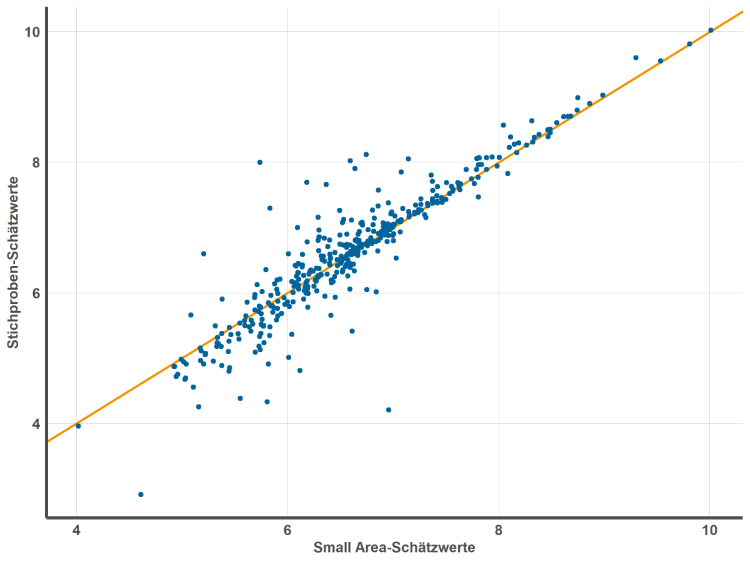
Im zweiten Schritt wollen wir anhand einer einfachen Grafik beurteilen, ob die Small Area-Schätzungen eine systematische Verzerrung aufweisen. Dazu tragen wir die teilweise mit hohen Schätzunsicherheiten behafteten, jedoch unverzerrten Stichproben-Schätzwerte sowie die Ergebnisse der Small Area-Schätzung aller Gemeinden in ein Streudiagramm ein (vgl. Abbildung 3). Falls keine systematische Verzerrung vorliegt, sollten die Datenpunkte der Gemeinden zufällig um die Winkelhalbierende streuen. Andernfalls sollte ein systematisches Muster der Streuung erkennbar sein. In Abbildung 3 ist jedoch allenfalls bei den Gemeinden mit eher niedrigem Mietniveau eine unwesentliche systematische Abweichung nach unten zu erkennen (d. h. der Small Area-Schätzer berechnet bei diesen Gemeinden tendenziell ein etwas niedrigeres Mietniveau als die Stichprobendaten).

_{Abbildung 3: Streudiagramm der Small Area-Schätzwerte und der Stichproben-Schätzwerte für das Berichtsjahr 2022}

Neben den beiden dargestellten Methoden zur Evaluation der Schätzergebnisse können (und sollten) weitere Instrumente der Modelldiagnostik angewendet werden (z. B. ein QQ-Plot zur Überprüfung der Modellannahmen).

Im Ergebnis lässt sich festhalten, dass die Small Area-Schätzung in unserer Anwendung grundsätzlich zum gewünschten Resultat einer Stabilisierung der Schätzergebnisse führt. Insbesondere können für die Gemeinden, für welche sich allein mit den vorliegenden Stichprobeninformationen kein verlässliches Schätzergebnis ableiten lässt, mit Hilfe der Small Area-Methodik trotzdem valide Schätzungen des Mietniveaus durchgeführt werden. Hierfür müssen geringfügige Verzerrungen bei der Schätzung in Kauf genommen werden.

Welche Erweiterungen der Small Area-Schätzungen können durchgeführt werden?

Erweiterung der Small Area-Schätzung um eine räumliche Komponente: Großstädte weisen im Allgemeinen ein höheres Mietniveau als eher ländlich geprägte Gegenden auf. Insbesondere in Ballungsgebieten wird jedoch auch das Mietniveau umliegender Gemeinden durch die direkte Nähe und Stadt-Umland-Beziehungen (z. B. Pendlerverflechtungen oder Stadt-Umland-Wanderungen) zu einer Großstadt beeinflusst. Dieser Effekt lässt sich durch eine Erweiterung der Small Area-Methodik in die Schätzung der durchschnittlichen Bruttokaltmiete einbeziehen. Dazu wird das Small Area-Schätzmodell in Schritt 2 um eine „Nachbarschaftsinformation“ für alle Gemeinden erweitert. Auch in unserer Veröffentlichung haben wir diese Erweiterung genutzt.

Berechnung von Schätzern für Gemeinden ohne Stichprobeninformationen: In Schritt 1 wurden Stichproben-Schätzwerte berechnet, die die Basis für die weitere Small Area-Schätzung bilden. Allerdings liegen für eine kleine Anzahl an Gemeinden überhaupt keine Stichprobeninformationen aus der Stichprobe des Mikrozensus vor. In einem solchen Fall können jedoch trotzdem Small Area-Schätzwerte berechnet werden, indem vollständig auf die Informationen aus den externen Kennzahlen zurückgegriffen wird. In Schritt 3 der Small Area-Schätzung erhalten diese für die betreffenden Gemeinden somit die Gewichtung 1. In unserer Veröffentlichung für das Berichtsjahr 2022 haben wir dieses Verfahren für insgesamt 18 Gemeinden genutzt.

Untersuchung zur Validität der Small Area-Methode

In einem Artikel im Wissenschaftsmagazin WISTA – Wirtschaft und Statistik (geplante Veröffentlichung: Juni 2026) vergleichen wir unsere Schätzergebnisse der durchschnittlichen Nettokaltmieten für die Gemeinden für das Berichtsjahr 2022 mit den Ergebnissen der Gebäude- und Wohnungszählung des Zensus 2022. Unsere Analyse zeigt, dass lediglich zufällige Abweichungen zwischen den Ergebnissen der Small Area-Schätzung und den Zensusergebnissen in moderater Höhe vorliegen, jedoch keine systematischen Verzerrungen der Schätzergebnisse festgestellt werden können. Dieser Befund liefert zusätzliche Evidenz für die Validität der Methode und unserer Schätzergebnisse.

Literaturhinweise

Alfken, C., Articus, C., Brenzel, H., Emmenegger, J., Münnich, R., Rohde, J. (2024): „Estimating Regional Rental Prices on LAU 2 Municipalities in North Rhine-Westphalia.“ In: Mingione, M., Vichi, M., Zaccaria, G. (eds) High-quality and Timely Statistics. CESS 2022. Studies in Theoretical and Applied Statistics. Springer, Cham. Abrufbar unter: https://doi.org/10.1007/978-3-031-63630-1_2
Articus, C.: „Small-Area-Verfahren zur Schätzung regionaler Mietpreise“, Wirtschaft und Statistik. Ausgabe 2/2014, Seite 113 ff.
Fay, R. E. und Herriot, R. A.: “Estimates of Income for Small Places: An Application of James-Stein Procedures to Census Data”, Journal of the American Statistical Association, Band 74/1979, Ausgabe 366, Seite 269 ff.
Münnich, R., Burgard, J. P. und Vogt, M.: Small Area-Statistik: Methoden und Anwendungen, AStA Wirtschafts- und Sozialstatistisches Archiv. Jahrgang 6, Seite 149 ff.

Daten zum Download

Ergebnisse_2018
xlsx (32.71 KB)

Results_2018
xlsx (32.61 KB)

Hilfsvariablen_2018
xlsx (103.43 KB)

Auxiliary Variables_2018
xlsx (103.46 KB)

Quellen der Hilfsvariablen_2018
xlsx (10.82 KB)

Sources of Auxiliary Variables_2018
xlsx (11 KB)

Ergebnisse Bruttokaltmiete_2022
xlsx (31.53 KB)

Ergebnisse Nettokaltmiete_2022
xlsx (33.38 KB)

Hilfsvariablen_2022
xlsx (188.45 KB)