Methodenbeschreibung: Kerndichteschätzer zur Veröffentlichung von Karten mit georeferenzierten Daten der amtlichen Statistik

 

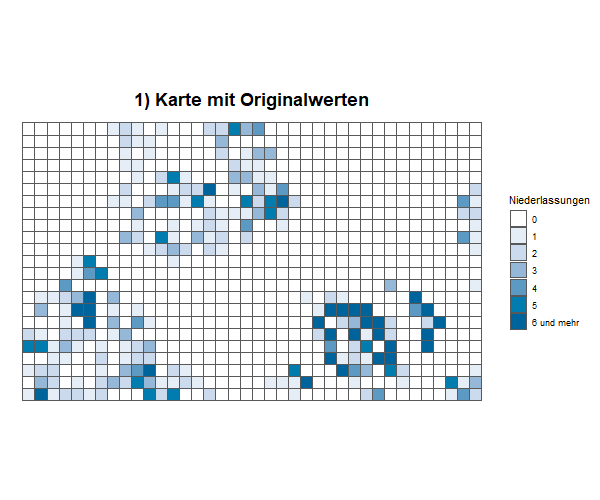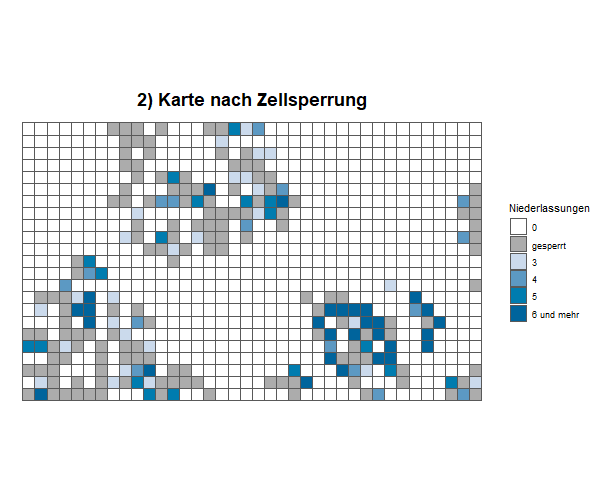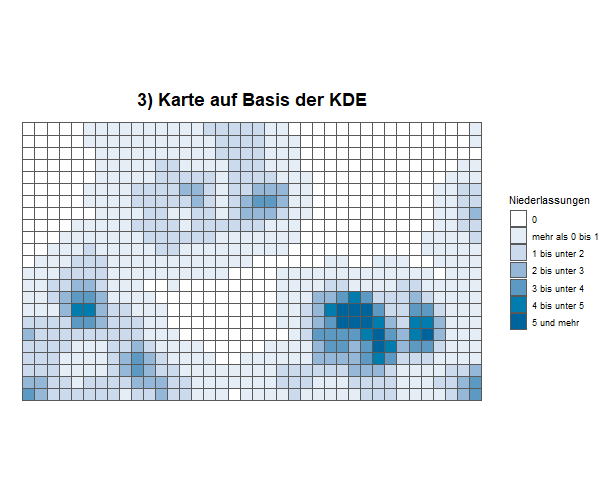
Die animierte Grafik visualisiert den Informationsgewinn, den eine Karte auf Basis einer KDE gegenüber einer Karte generieren kann, bei der gering besetzte Zellen gesperrt werden müssten, um Einzelangaben zu schützen.

 

1) Karte mit Originalwerten: Die Intensität des Farbtons in einer Zelle symbolisiert die zugehörige Anzahl an Einheiten. Viele Zellen weisen sehr kleine Fallzahlen auf, die potenziell eine Aufdeckung von zugrundeliegenden Einzelangaben ermöglichen.

2) Karte nach Zellsperrung: Alle Zellen, zu denen weniger als eine bestimmte Mindestanzahl an Einheiten beitragen, müssen gesperrt werden (ausgegraute Zellen). Für die Nutzerinnen und Nutzer gehen dadurch viele Informationen verloren.

3) Karte auf Basis der KDE: Zu jeder Zelle ist ein Wert verfügbar. Sperrungen ganzer Zellen sind nicht notwendig. Für die Nutzerinnen und Nutzer sind Regionen mit hoher und niedriger Dichte des dargestellten Merkmals auf den ersten Blick erkennbar.

 

Was ist der Vorteil der Verwendung der Kerndichteschätzung für georeferenzierte Daten?

 

Mithilfe der Anwendung der KDE ist es möglich, ein größeres Spektrum an Auswertungen auf Basis kleinräumiger, georeferenzierter Daten unter Wahrung der Qualitätsstandards der amtlichen Statistik zu veröffentlichen. Die Anwendung auf georeferenzierte Daten der amtlichen Statistik dient insofern nicht der Schätzung einer unbekannten Verteilung, sondern hat zum Ziel, die kleinräumige Darstellung von amtlichen Daten in Gitterzellen zu ermöglichen, die sowohl keinerlei Rückschlüsse auf Einzelangaben erlaubt als auch anschaulich und intuitiv ist.

 

Die KDE bietet damit eine Alternative zur bisher in der amtlichen Statistik weit verbreiteten Anonymisierungsmethode der sogenannten Zellsperrung. Bei der Zellsperrung werden zunächst alle Tabellenfelder bzw. Gitterzellen gesperrt, die einen Rückschluss auf Einzelangaben ermöglichen. Da jedoch zusätzlich weitere, eigentlich unkritische Tabellenfelder bzw. Gitterzellen gesperrt werden müssen, um die kritischen Ergebnisse zu schützen, muss häufig darüber hinaus eine Vielzahl an Ergebnissen gesperrt werden. Dadurch wird der Informationsgehalt insbesondere von auf Gitterzellen basierenden Kartendarstellungen stark eingeschränkt. Für die Nutzerinnen und Nutzer amtlicher georeferenzierter Daten stellt dies einen wesentlichen Nachteil dar.
 

Was unterscheidet eine Kartendarstellung auf Basis einer Kerndichteschätzung von gewohnten Kartendarstellungen?

 

Aus bisher veröffentlichten Kartendarstellungen der amtlichen Statistik sind die Nutzerinnen und Nutzer gewohnt, dass jede Gitterzelle eine Farbcodierung aufweist, auf deren Basis sich auf die exakte oder ungefähre Anzahl der zu dieser Gitterzelle beitragenden Fälle schließen lässt (z. B. „In Zelle X gibt es zwischen fünf und zehn Niederlassungen im Wirtschaftszweig Verarbeitendes Gewerbe“). Auch Mittelwerte einer Gitterzelle können für bestimmte Sachverhalte ausgewiesen werden (z. B. „Die durchschnittliche Beschäftigtenzahl aller Niederlassungen in Zelle Y beträgt 12“).

 

Im Gegensatz dazu bilden bei einer Kartendarstellung auf Basis einer KDE die sogenannten Kerndichtewerte die Grundlage der Farbcodierung der einzelnen Gitterzellen. Auch hierbei korrespondiert die Intensität des ausgewiesenen Farbtons (siehe Abschnitt „Visualisierung (Zuweisung der Farbtöne)“ im nachfolgenden Aufklappfeld) zwar direkt mit der Anzahl der Fälle bzw. der Höhe des Mittelwerts für diese Gitterzelle, jedoch wird ein Rückschluss auf den exakten – ggf. zu schützenden – Wert der Gitterzellen verhindert. Die Nutzerinnen und Nutzer können damit auf einen Blick die regionale Verteilung erfassen sowie lokale Schwerpunkte oder Regionen mit schwacher Ausprägung des dargestellten Sachverhalts identifizieren, ohne dass ein Risiko einer Aufdeckung von Einzelangaben der Auskunftgebenden besteht (siehe auch Animation oben).
 

Welche Schritte werden durchgeführt, um zu einer Kartendarstellung auf Basis einer Kerndichteschätzung zu gelangen?

 

Um eine farbcodierte Kartendarstellung auf Basis der KDE zu erzeugen, sind verschiedene Schritte auszuführen. Dieses Vorgehen wird im Folgenden anhand einfach aufgebauter Grafiken visualisiert. Zwar weisen georeferenzierte Daten stets zwei geografische Dimensionen auf (Längen- und Breitenkoordinate), allerdings lässt sich die Methodik der KDE anhand einer eindimensionalen Darstellung leichter nachvollziehen. In unseren Abbildungen beschränken wir uns daher auf die gemeinsame Darstellung beider Dimensionen auf der x-Achse der Grafiken.

 

Folgende Schritte sind zur Erzeugung einer farbcodierten Karte auf Basis einer KDE durchzuführen:

 

– Darstellung der Datenpunkte: Jeder Datenpunkt wird auf Basis seiner Geokoordinaten an seine entsprechende Position in die Gitterzellen eingetragen. Die Datenpunkte unserer fiktiven Stichprobe mit fünf Beobachtungen sind in Abbildung 1 jeweils durch einen Strich auf der x-Achse dargestellt. Die (eigentlich zweidimensionalen) Gitterzellen werden durch die mit hellgrauen Linien abgegrenzten Intervalle visualisiert.
 

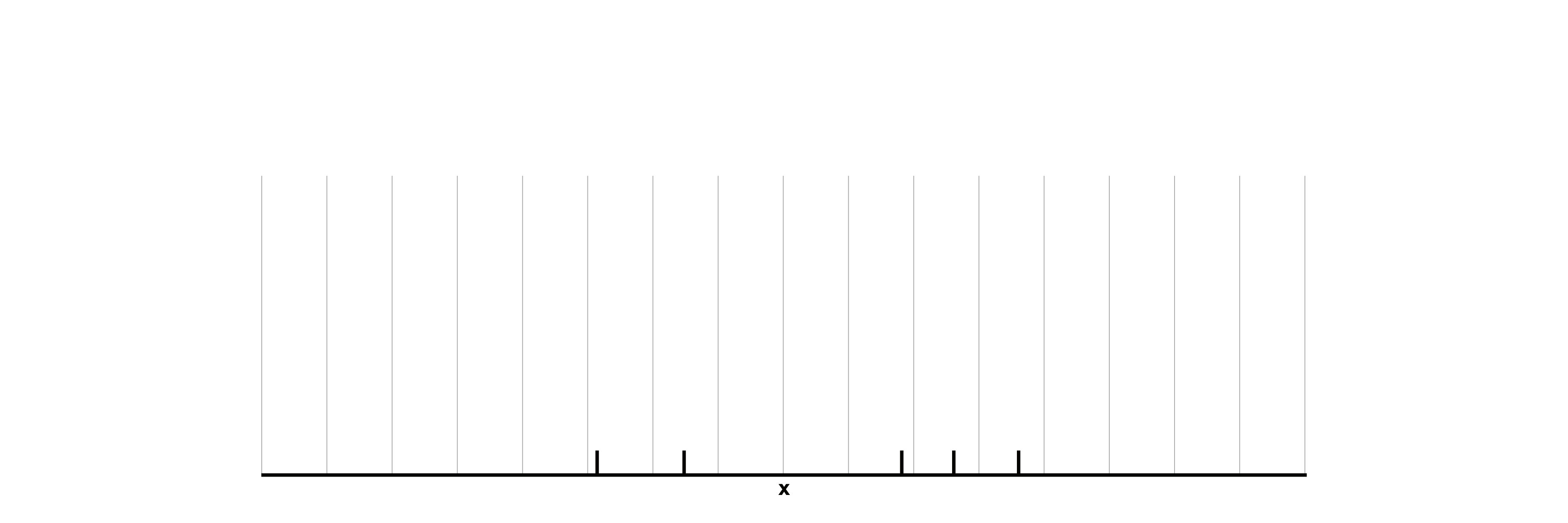
Abbildung 1: Im ersten Schritt werden alle Datenpunkte (schwarze Striche) in die Gitterzellen (vertikale hellgraue Linien) eingetragen.

 

– Überlagerung der Datenpunkte mit Kernfunktionen: Über jeden einzelnen Datenpunkt wird nun jeweils eine symmetrische Modellfunktion gelegt (vgl. Abbildung 2). Den größten Funktionswert weist diese Funktion jeweils an der Stelle auf der x-Achse auf, wo sich der jeweilige Datenpunkt befindet. Würde man seitlich auf die entsprechende Gitterkarte schauen, würde sich über jeden Datenpunkt ein symmetrischer Berg erheben, der vom „Gipfel“ aus in alle Richtungen identisch abfällt. Diese Modellfunktion wird als „Kern“ bezeichnet und im Abschnitt „Wahl der Kernfunktion“ im übernächsten Aufklappfeld näher beschrieben. Das Volumen, das ein Kern unterhalb seines Funktionsverlaufs einschließt, beträgt für jeden einzelnen Kern eins. Alternativ kann das Volumen auch dem Wert des Datenpunktes entsprechen, wenn Wertmerkmale (z. B. Anzahl der Arbeitnehmerinnen und -nehmer einer Niederlassung) dargestellt werden.

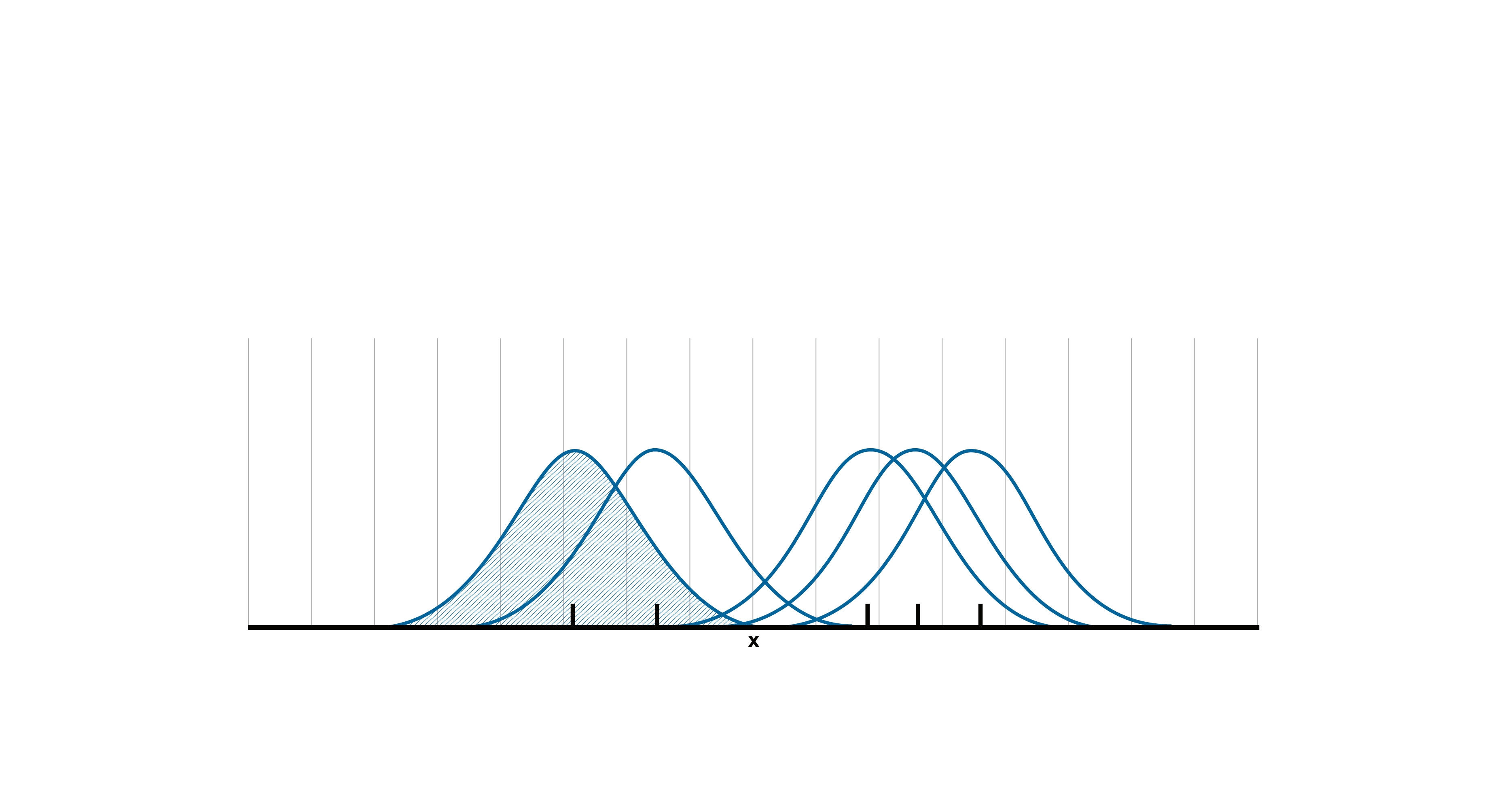
Abbildung 2: Über jeden Datenpunkt wird eine symmetrische Funktion gelegt – der „Kern“ eines Datenpunktes. Mittelpunkt und maximaler Funktionswert befinden sich jeweils an der Stelle, wo der zugehörige Datenpunkt liegt. Die einzelnen Kerne überschreiten Gittergrenzen und überschneiden sich mit anderen Kernen. Das Volumen im realen mehrdimensionalen Fall entspricht der Fläche  unterhalb des Kerns in dieser vereinfachten zweidimensionalen Darstellung (siehe schraffierte Fläche).

 

Zu beachten ist, dass ein Kern stets die Grenzen der Gitterzelle, in welcher der zugehörige Datenpunkt liegt, überschreitet. Dies ist in Abbildung 2 ersichtlich: Die Kerne aller fünf eingezeichneten Datenpunkte überschreiten hier gleich mehrere Gittergrenzen (durch vertikale graue Linien visualisiert). Das Volumen, das jeder einzelne Kern einschließt, beschränkt sich somit nicht nur auf die jeweilige Ausgangsgitterzelle, sondern wird auch auf angrenzende Gitterzellen aufgeteilt.

 

– Berechnung zellenspezifischer Volumenwerte (Kerndichten): Wie im Beispiel in Abbildung 2 dargestellt, führt die Überschreitung von Gittergrenzen der Kerne dazu, dass in viele Gitterzellen Teile von Kernen fallen, die zu unterschiedlichen Datenpunkten gehören – auch Kerne solcher Datenpunkte, die eigentlich in einer benachbarten Gitterzelle lokalisiert sind.

 

Somit lässt sich für jede einzelne Gitterzelle ein Gesamtvolumenwert berechnen, der sich aus der Summe aller Volumenteile derjenigen Kerne ergibt, die in die betreffende Gitterzelle fallen. Ein Datenpunkt trägt dabei mit seinem Kern umso mehr zu einem Volumenwert einer Gitterzelle bei, je näher dieser Datenpunkt zum Mittelpunkt der Gitterzelle gelegen ist. Den Volumenwert, der einer Gitterzelle zugewiesen wird, bezeichnen wir als „Kerndichte“ dieser Gitterzelle.

 

Zu beachten ist, dass die Kerndichte einer Gitterzelle damit direkt von der Anzahl der in der unmittelbaren Nähe befindlichen Datenpunkte abhängt – also Datenpunkten, die entweder in der eigenen Gitterzelle oder in den benachbarten Gitterzellen liegen. Durch die Addition vieler einzelner Volumenwerte an jedem Punkt eines Gitters ergibt sich eine stetige („glatte“) Funktion. Abbildung 3 zeigt eine solche geglättete Funktion in zweidimensionaler Darstellungsweise.
 

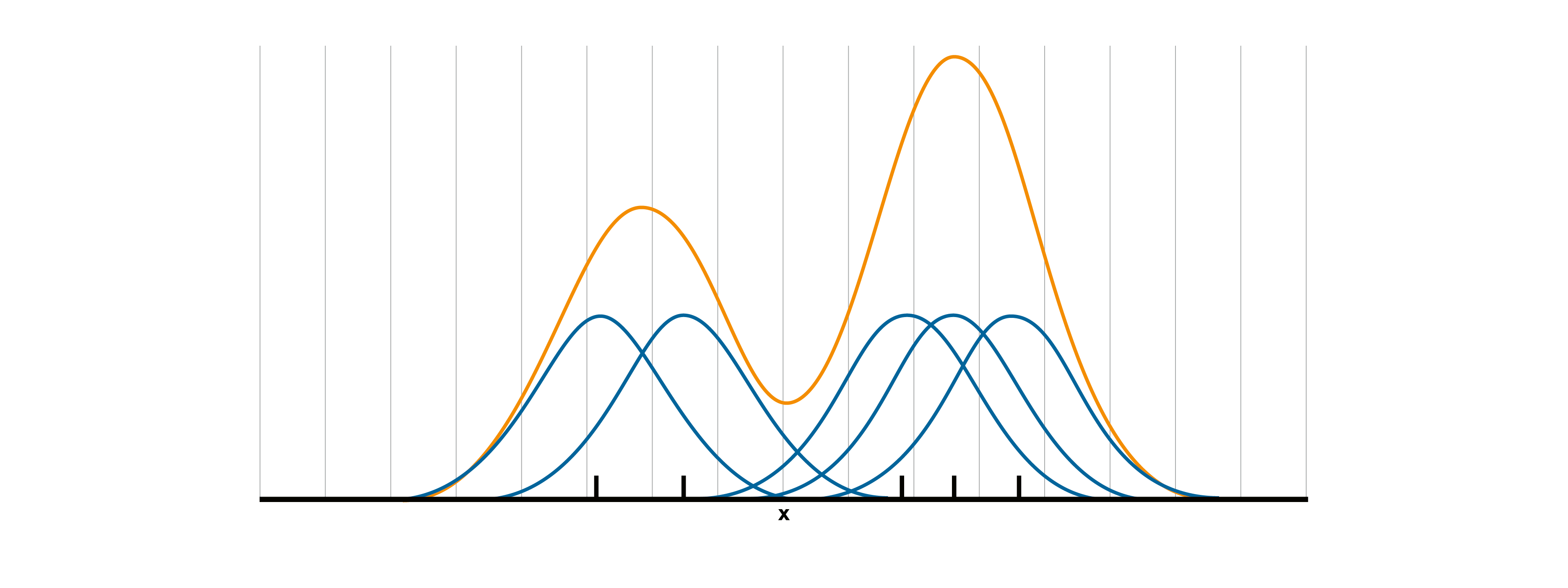
Abbildung 3:

An jeder Stelle der x-Achse werden die realisierten Funktionswerte aller Kerne (blau) aufsummiert.Es ergibt sich eine stetige Funktion (schwarz) und an jeder Stelle auf der x-Achse eine geschätzte Kerndichte. Die Kerndichte für eine gesamte Gitterzelle ergibt sich aus dem Volumenwert, den die geschätzte Funktion in jeder Gitterzelle einschließt – in dieser Darstellung entspricht die Kerndichte einer Gitterzelle jeweils der Fläche zwischen der geschätzten Funktion (schwarz) und der x-Achse.

 

– Visualisierung (Zuweisung der Farbtöne): Nachdem jeder Gitterzelle eine Kerndichte zugewiesen wurde, wird der Wert der Kerndichte jeder Gitterzelle in einen Farbcode übersetzt. Um einen direkten Rückschluss von einem Farbton zu einem genauen Kerndichtewert zu verhindern, erfolgt eine in Intervallen gestaffelte Zuweisung der Farbtöne auf Basis der Werte der Kerndichten. Dies veranschaulicht folgendes fiktives Beispiel:

 

In einer Karte soll auf Ebene von 1 km²-Gitterzellen die Anzahl der dort lokalisierten Niederlassungen mittels einer KDE dargestellt werden. Die für jede Gitterzelle geschätzten Kerndichten (also die Volumenwerte jeder Zelle) werden in fünf überlappungsfreie Klassen gestaffelt. Den Klassen wird das folgende Farbschema zugeordnet:

 

 

Ein und derselbe Blauton wird beispielsweise allen Gitterzellen zugewiesen, die einen Kerndichtewert im Intervall [2.5; 5] aufweisen. Ein Rückschluss auf den exakten Kerndichtewert ist auf Basis des Farbtons nicht möglich. Bei der Interpretation der Kerndichten ist zu berücksichtigen, dass eine Kerndichte nicht exakt mit der Anzahl der in einer Gitterzelle lokalisierten Niederlassungen übereinstimmt, sondern lediglich die Größenordnung dieser Anzahl wiedergibt.

 

Außerdem ist in der Regel eine für jede Kartendarstellung individuelle Farbfestlegung zu beachten. Ein und derselbe Farbton kann in zwei unterschiedlichen Karten verschiedenen Intervallen von Kerndichten zugeordnet werden.

 

Wie lässt sich der Kerndichtewert einer Gitterzelle interpretieren?

 

Ein Kerndichtewert entspricht natürlich nicht exakt der originalen Anzahl bzw. dem originalen Wert der in der Gitterzelle befindlichen Datenpunkte. Dies soll gerade durch die Anwendung der KDE verhindert werden, um den Schutz vor Aufdeckung einer Einzelangabe zu gewährleisten. Zudem ist der Wert einer Kerndichte in der Regel nicht ganzzahlig. Vielmehr soll dieser (bzw. der zugewiesene Farbton) widerspiegeln, wie viele Datenpunkte sich in unmittelbarer Nähe der betreffenden Gitterzelle befinden, d. h. in dieser Gitterzelle oder in einer benachbarten Gitterzelle. Auch ist entscheidend, wie nah der Datenpunkt am Mittelpunkt der Gitterzelle lokalisiert ist.

 

Eine quantifizierbare Interpretation eines Kerndichtewerts liefert am ehesten das Konzept des Erwartungswerts: Der aufsummierte Volumenwert über alle zu einer Gitterzelle beitragenden Kerne kann als die Anzahl an Datenpunkten (bzw. deren Wertigkeit) interpretiert werden, die anhand der vorliegenden Stichprobe in einer gegebenen (fiktiven) Grundgesamtheit für diese Gitterzelle zu erwarten wären. Hiermit schließt sich auch der Kreis zur eigentlichen Verwendung der KDE in der Statistik: die Schätzung einer Verteilung in der Grundgesamtheit (und damit auch eines Erwartungswerts) auf Basis einer vorliegenden Stichprobe.
 

Wodurch wird das Ergebnis einer Kerndichteschätzung beeinflusst?

 

Wie bei den meisten statistischen Methoden hängt auch das genaue Ergebnis der KDE von Festlegungen zur Darstellungsweise sowie von Verfahrensparametern ab. Abhängig von der konkreten Ausgestaltung der KDE kann deren Ergebnis im Detail variieren. In unserer Anwendung der KDE müssen insgesamt vier Festlegungen getroffen werden:

 

– Wahl der Klassifikation eines Merkmals: Da das visuelle Erscheinungsbild der Karte wesentlich von der gewählten Klassifikation des dargestellten Merkmals abhängt, muss festgelegt werden, in wie viele Intervalle die Kerndichtewerte gestaffelt werden und wie viele unterschiedliche Farbtöne die farbcodierte Karte folglich enthalten soll. Bei der Wahl der Klassifikation ist Folgendes zu berücksichtigen: Eine höhere Anzahl an Intervallen ermöglicht zwar eine umso genauere Darstellung des Sachverhalts, eine zu große Genauigkeit erlaubt unter Umständen jedoch wiederum einen Rückschluss auf schützenswerte Einzeldaten. Im obigen Beispiel im Abschnitt „Visualisierung (Zuweisung der Farbtöne)“ wurde für das Merkmal „Anzahl der Niederlassungen“ eine Klassifikation mit fünf Klassen gewählt.

– Wahl der Größe der Gitterzellen: Für die Darstellung einer farbcodierten Karte auf Basis der KDE ist außerdem die Größe der Gitterzellen ein entscheidendes auswählbares Kriterium. Größere Kantenlängen der Gitterzellen führen unmittelbar zu höheren Kerndichtewerten und beeinflussen damit direkt den einer Gitterzelle zugewiesenen Farbton. In der amtlichen Statistik werden die normierten INSPIRE-Rastergitter in den Größen 100 m×100 m, 1 km×1 km sowie 5 km×5 km verwendet. Um einen zu genauen Rückschluss auf schützenswerte Einzeldaten zu vermeiden, sollte die Wahl der Gitterzellengröße gemeinsam mit der Wahl der Klassifikation getroffen werden.

 

– Wahl der Kernfunktion: Im obigen Abschnitt „Überlagerung der Datenpunkte mit Kernfunktionen“ im dritten Aufklappfeld wurde der Kern bislang nur allgemein als symmetrische und stetige Funktion beschrieben, mit welcher ein Datenpunkt überlagert wird. Tatsächlich stellt jeder Kern eine Wahrscheinlichkeitsdichtefunktion dar – deshalb verfügt jeder Kern auch über ein Volumen von eins (= 100 Prozent „Wahrscheinlichkeit“). Als Kern kann grundsätzlich eine Vielzahl verschiedener Dichtefunktionen verwendet werden. Die Wahl der Kernfunktion bestimmt u. a., wie stark der Einfluss der vom Gitterzellenmittelpunkt entfernt lokalisierten Datenpunkte auf die Kerndichte einer Gitterzelle ist. In Veröffentlichungen des Statistischen Landesamtes Nordrhein-Westfalen wird für die Verarbeitung der georeferenzierten Daten standardmäßig ArcGis eingesetzt, das den Epanechnikov-Kern verwendet.
 

 

Liste häufig verwendeter Kernfunktionen in eindimensionaler Darstellung

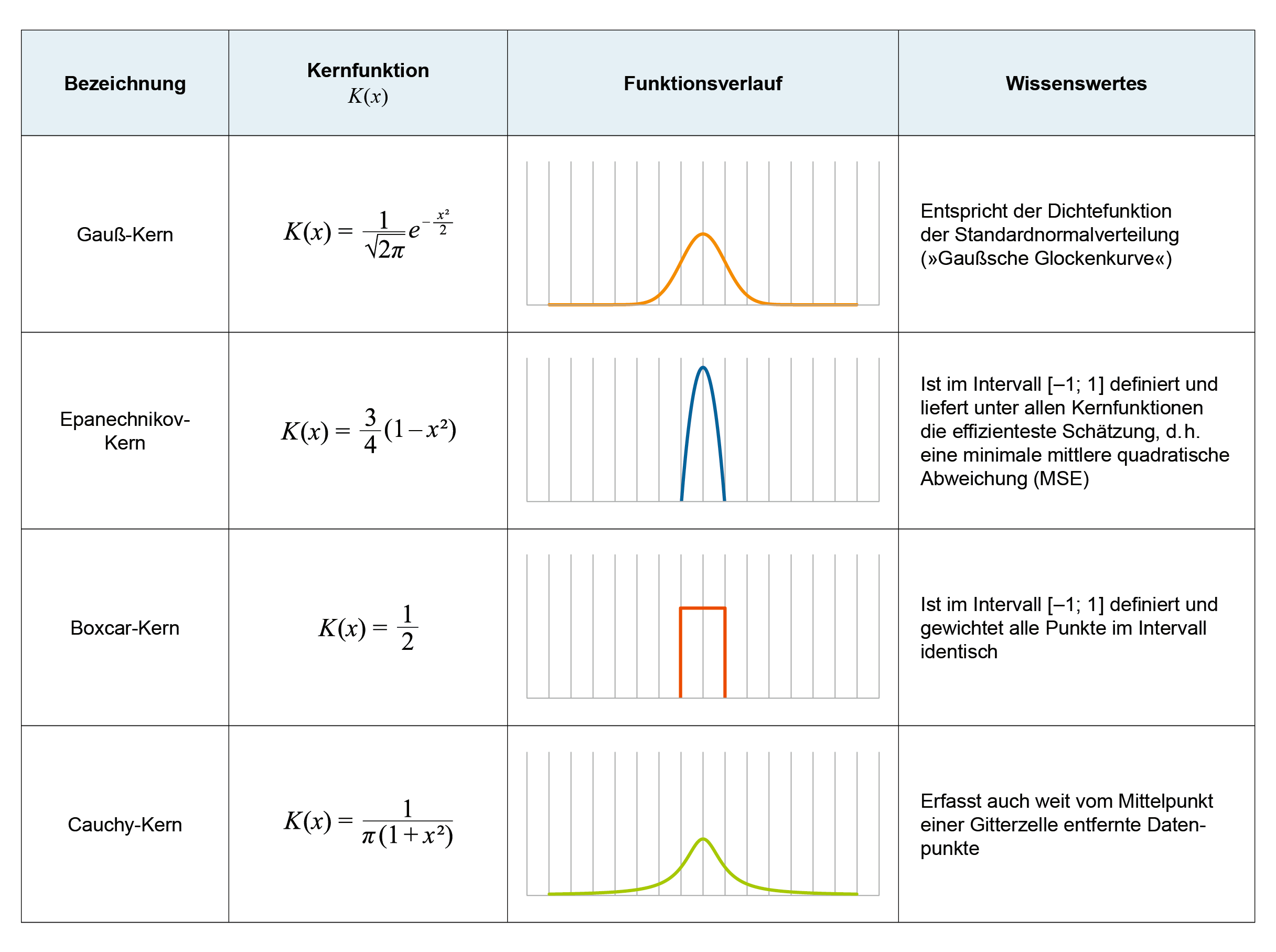
Anmerkung: Um die formale Komplexität zu begrenzen, beschränken wir uns hier auf die Darstellung des eindimensionalen Falls. Das grundlegende Aussehen der Kernfunktionen wird daduch – abgesehen von deren Dimensionalität – nicht beeinflusst.

 

– Wahl der Bandbreite: Die Bandbreite stellt einen wählbaren Parameter der KDE dar, welcher für die Stauchung bzw. Streckung der verwendeten Kernfunktion verantwortlich ist. Die Bandbreite kann als der Suchradius um einen Mittelpunkt einer Gitterzelle angesehen werden. Die Kerndichte eines Datenpunkts erreicht dabei den Wert null, sobald der Rand des Suchradius erreicht ist. Zwar lässt sich die Bandbreite theoretisch frei wählen, allerdings beeinflusst die verwendete Bandbreite die Qualität des Ergebnisses einer KDE so stark, dass sich de facto Beschränkungen für die Wahl der Bandbreite ergeben.

 

In Abbildung 4 wird dieser Aspekt visualisiert. Dazu nehmen wir an, dass wir mittels einer KDE die Wahrscheinlichkeitsverteilung einer Grundgesamtheit schätzen möchten und es sich bei dieser (in der Realität uns natürlich unbekannten) Verteilung um eine Standardnormalverteilung handeln würde. Für die vorzunehmende KDE liegt uns eine Stichprobe vor, die auf Basis der Standardnormalverteilung generiert wurde und in der Abbildung durch blaue Striche auf der x-Achse visualisiert ist. Wir führen nun drei KDE mit jeweils unterschiedlicher Bandbreite durch, um die in der Abbildung in Grau dargestellte Standardnormalverteilung möglichst adäquat zu schätzen:

 

– Die in Orange dargestellte KDE mit einer zu klein gewählten Bandbreite resultiert in einer geschätzten Funktion, die nicht geglättet erscheint und viele falsche Datenartefakte enthält.
   

– Bei der in Grün dargestellten KDE mit zu groß gewählter Bandbreite kommt es hingegen zu einer Überglättung, sodass ein Großteil der zugrundeliegenden Struktur der grauen Funktion nicht abgebildet wird.
   

– Einen Kompromiss liefert eine „mittlere“ Bandbreitenwahl: Die in Schwarz dargestellte KDE liefert eine angemessene Schätzung der in Grau dargestellten (und in der Realität unbekannten) Standardnormalverteilung.
 

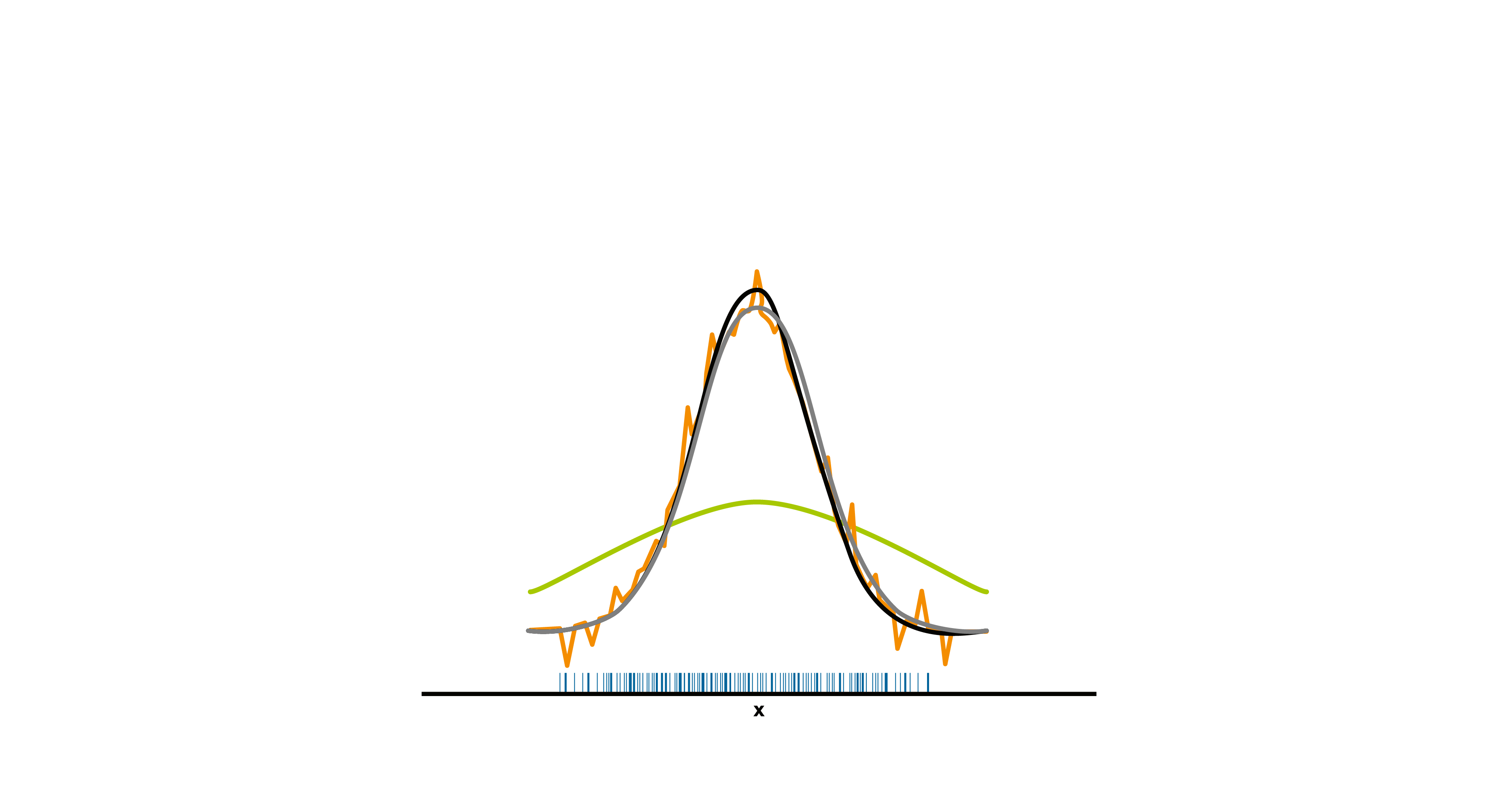
Abbildung 4:

Drei KDE mit unterschiedlicher Bandbreite werden zur Schätzung der Standardnormalverteilung (graue Funktion) durchgeführt. Die Qualität der Schätzungen hängt stark von der verwendeten Bandbreite ab. Die zugrundeliegende Stichprobe wird durch die blauen Striche auf der x-Achse visualisiert.

 

In der Praxis wird die Bandbreite zur Durchführung einer KDE daher häufig mittels Faustformeln bestimmt. Für unsere Anwendungen wird die Bandbreite ebenfalls anhand einer gängigen Formel berechnet.

 

Die Berechnung der Bandbreite h > 0 für eine KDE erfolgt in unseren Anwendungen durch die Formel:

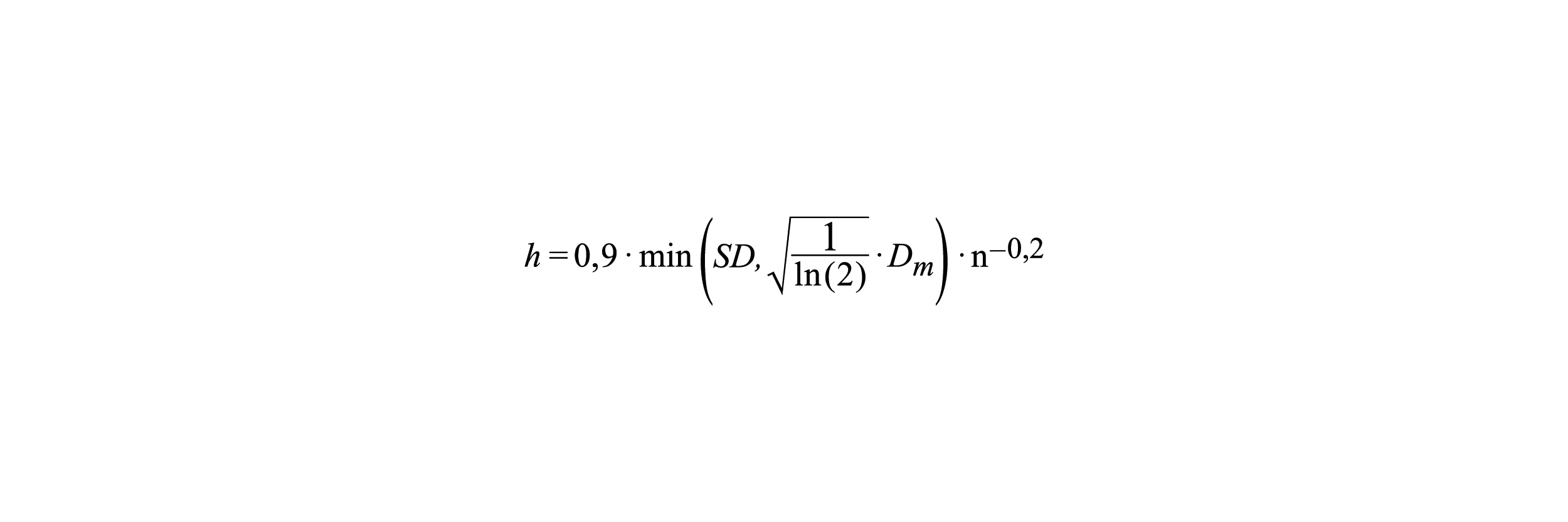
Dabei bezeichnet n die Anzahl der Datenpunkte. Die sogenannte Standardentfernung SD der Koordinaten (xi,yi ) aller Datenpunkte i = 1,…, n vom jeweiligen Zellenmittelpunkt (x̅, y̅) berechnet sich durch:

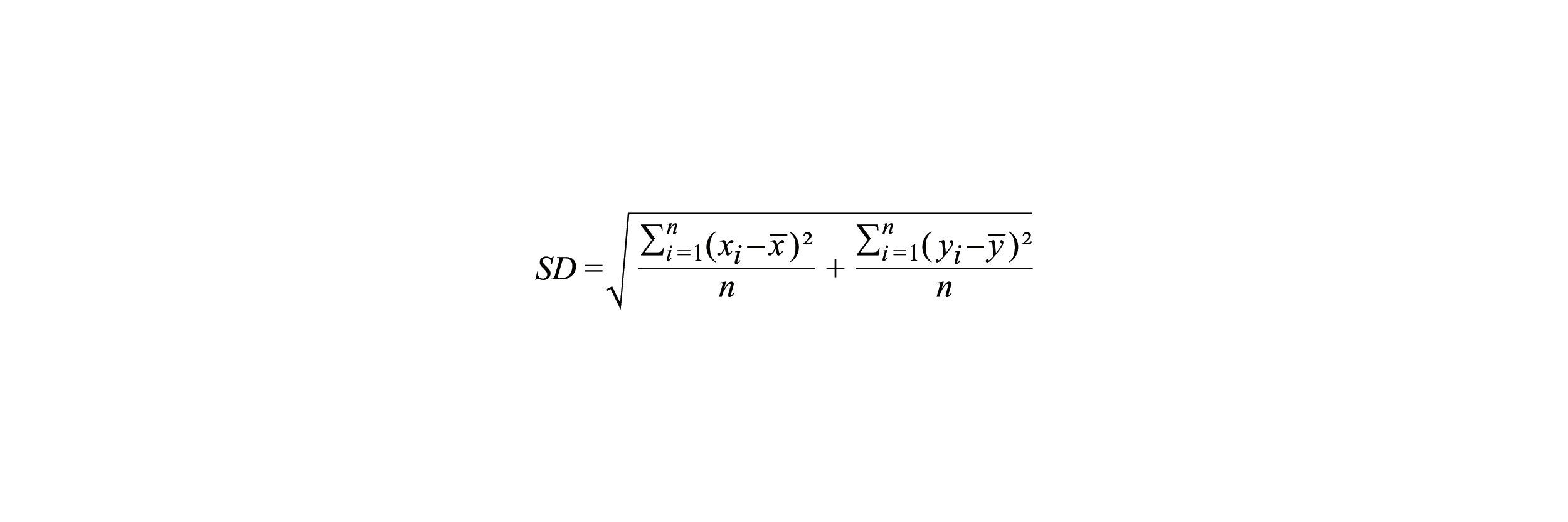
Zudem stellt Dm den Medianwert der Entfernung der Datenpunkte vom jeweiligen Zellenmittelpunkt dar. Die sogenannte Minimumfunktion min() nimmt stets den kleineren der beiden in der Klammer dargestellten Werte an. Die für eine KDE in Frage kommenden Bandbreiten hängen zudem von der Gittergröße (siehe obiger Abschnitt „Wahl der Größe der Gitterzellen“) ab.

 

Sobald alle vier Festlegungen zur Darstellung und Parametrisierung der KDE getroffen sind, kann die KDE für den vorliegenden Datensatz durchgeführt werden. Um einen Volumenwert für jede Gitterzelle zu bestimmen, wird für jede Stelle in jeder Gitterzelle ein Dichtewert geschätzt, sodass ein „glatter“ Funktionsverlauf entsteht.

 

Berechnung der Kerndichte

 

Mit der Kernfunktion K (x) und der Bandbreite h > 0 wird die Kerndichte f ̃(⋅ ; h) auf Basis der vorliegenden Stichprobe x1,…,xn an jeder Stelle x folgendermaßen bestimmt:

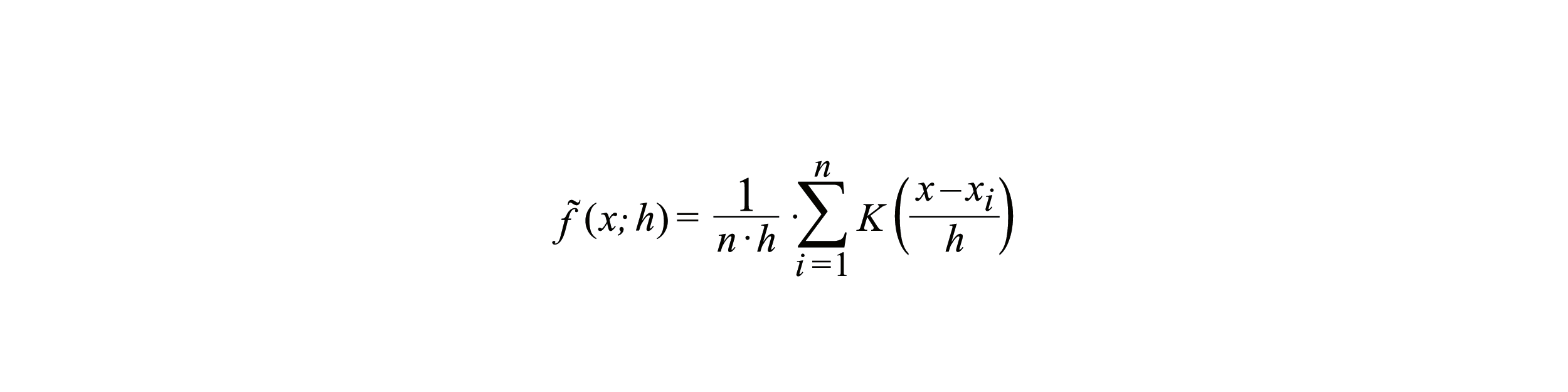
Anmerkung: Um die formale Komplexität zu begrenzen, beschränken wir uns hier auf die Darstellung des eindimensionalen Falls. Das grundlegende Vorgehen bei der Berechnung wird durch die Vereinfachung – abgesehen von der notwendigen Berücksichtigung der Mehrdimensionalität – nicht beeinflusst.

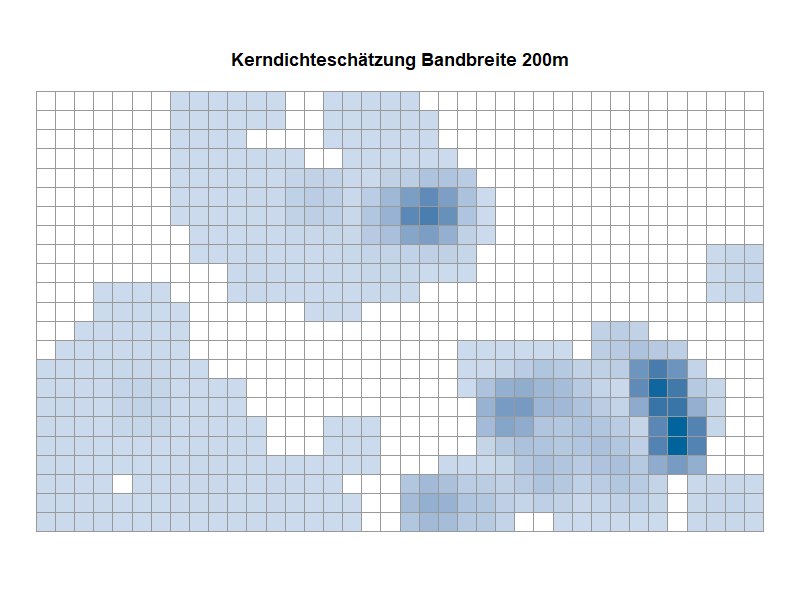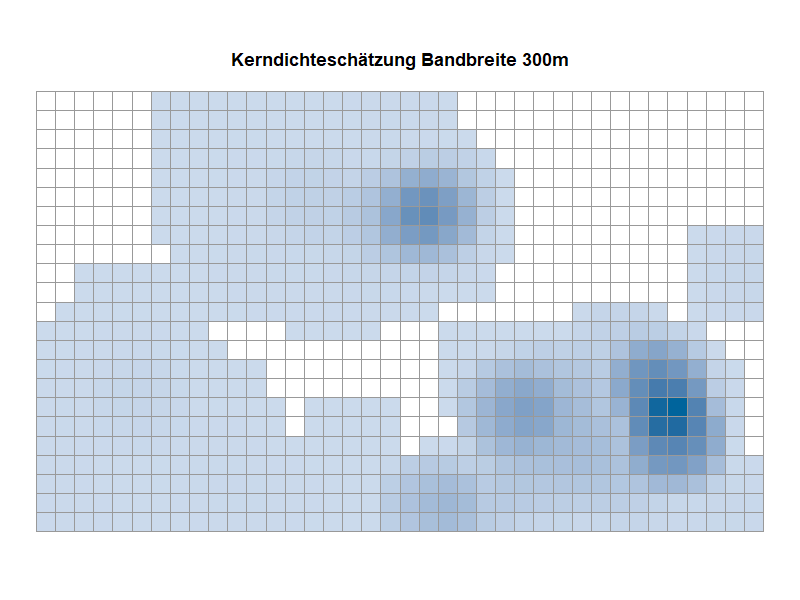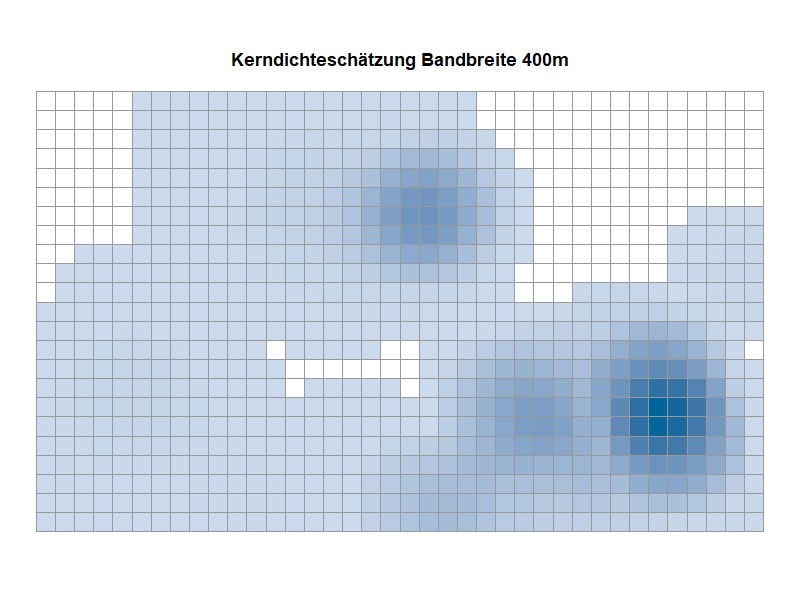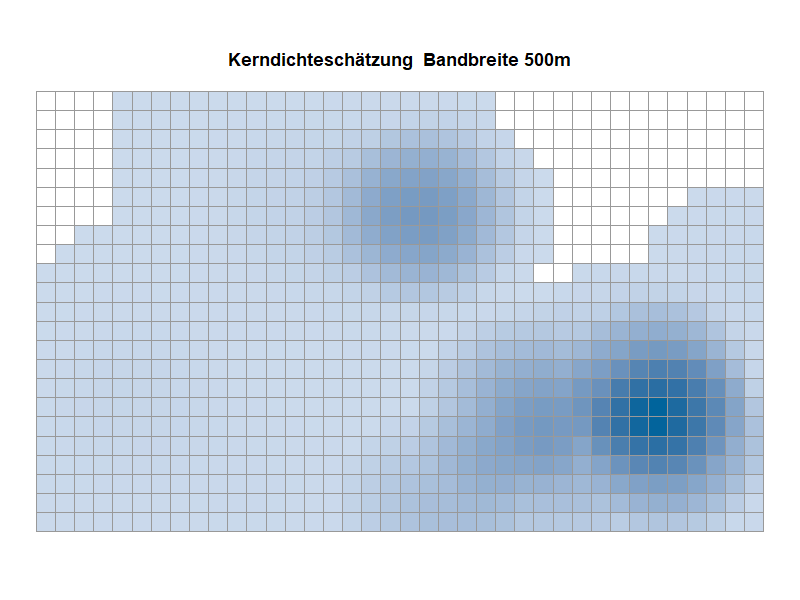
Kerndichteschätzung: Varianten im Vergleich (Animation) 

 

Die Animation eines Kartenausschnitts zeigt die Ergebnisse der Kerndichteschätzung auf der Basis verschiedener Bandbreiten. Es wird sichtbar, welche Auswirkungen die Wahl der Bandbreite auf die Visualisierung hat. Be­achten Sie die Ver­änder­ung in der Fläche mit zu­nehmender Band­breite.

Kerndichteschätzer zum Ausprobieren